Mathematical Derivation of Rule of 72 in Finance
Rule of 72 or Rule of 70 or doubling rule is a well known rule in finance. In this post, we first see how this rule works and from where it is derived.
Rule of 72 or Rule of 70:
If a capital is invested and compounded at the rate of r %/year, it will be doubled (2P) approximately in (70/r) years or (72/r) years.
For example, if a capital 100 is invested and compounded at the rate of 10%/year, it would be doubled approximately in
(70/10)years or (72/10) years
i.e. 7 years or 7.2 years.
i.e. if a capital 100 is invested and compounded at the rate of 10%/year, it will be doubled i.e . 200 approximately in 7 years or 7.2 years.
NOTE:
The time derived from Rule of 70 or Rule of 72 is a approximation. Of course, a good approximation i.e. it is very closer to the real value.
Mathematical Formula of Compound Interest:
If,
P= Principal
A= Amount (Principal + Compound interest)
r= Rate of interest
n= Number of year, capital remain invested
it is given by
Now, we take the same example and apply in mathematical formula to find the year.
The question was 100 is invested and compounded at the rate of 10%/year. We have to find the time for doubling.
Here,
P= 100
A= 100×2=200
r=10
n= ?
So, actual time of doubling the capital is 7.2725 years.
From the above calculation, it is clear that Rule of 70 or Rule of 72 provides a good approximation for daily life use.
Now, we see how Rule of 70 or Rule of 72 is derived mathematically.
Mathematical derivation of Rule of 72 or Rule of 70:
Let,
P= Principal
A= Amount (Principal + compound interest)
r= rate of interest per year
n= year of investment
We have,
Let, money will be doubled in n years.
A=2P in n years.
So,
Now, we have to simplify the above expression. For that we have to simplify the term ln(1+ r/100). Hence, we have to do some approximation.
We have,
if, 0<x<<1
x2 <<<1
Hence, for very small value of x, higher order of x can be neglected.
So, for very small value of x, we can write,
ln(1+x)≈x ..........(ii)
Now,
if, 0<r<<100
the, 0<(r/100)<<1
From, equation (i),
So,
Now, we look further at the expansion of ln(1+x)
If , 0<x<1
So, it is clear that,
ln(1+x)<x (but, of-course ln(1+x) is closer to x)
Now, if we take ln(1+x)=x , we are taking slightly higher value.
Let's look at the equation (i)
If we take,
We are taking slightly higher value in denominator. So, remaining the ratio same, we have to increase numerator, in this case 0.69315 .
So, if we modify the equation (iii), it would be
Now,
70 is divisible by
1,2,5,7,10,14,35 .
And 72 is divisible by
1,2,3,4,6,8,9,12,18,24,36.
Since, 72 has more factors than 70, it would be better to use 72.
Further, we have to keep in mind that Rule of 70 or Rule of 72 is give a approximate result. But, obviously, that approximation is worthy for daily life use.
Words which has different meaning in Science and in Daily life use


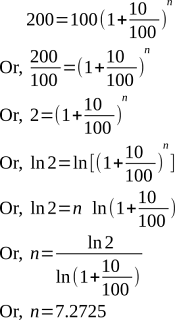


.png)

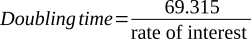
.png)
%20lees%20.png)




Comments
Post a Comment